What is Hydrogen cracking or cold cracking or Delayed Cracking?
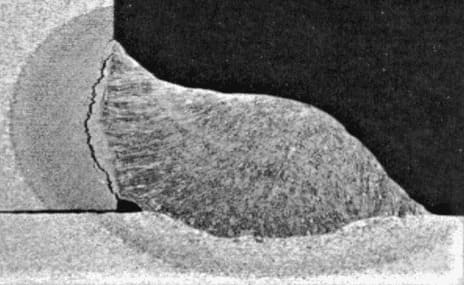
Hydrogen Induced Cracking (HIC) which is commonly known as Hydrogen cracking or Delayed Cracking or Cold cracking occurs in carbon or low-alloy steels (If I say precisely it is Ferritic Steels) when atomic hydrogen diffuses into it and forms molecular hydrogen during Welding of Carbon steel and low alloy steels. .
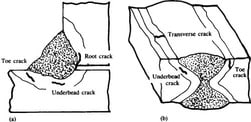
It is caused by the diffusion of hydrogen to the higher stresses, hardened part of the weldment.
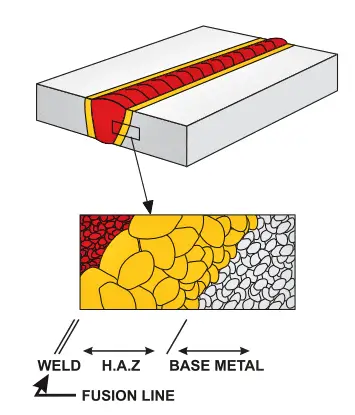
They occur generally in Heat Affected Zone (HAZ) in C-Mn steels but can extend to the weld metal as there is a greater risk of forming a brittle microstructure in the HAZ, most of the cold cracks are to be found in the parent metal. Fewer changes in the weld metal as welding consumables contain lower carbon content.
Hydrogen gets dissolve in the weld during welding & present is some amount. The source of this hydrogen are from the welding rod (in stick welding & Flux Cored Arc Welding), flux (in Submerged Arc Welding & Electro Slag Welding), moisture on base metal or from the shielding gas. A high level of humidity in the atmosphere can also induce hydrogen in the welding pool.
Why we say it Cold cracking or Delayed Cracking
Hydrogen Cracking is also called Cold cracking as the cracks occurs when the welding has cooled down to temperature below 100°C (Cold cracking does not occur when the welding is hot or during weld solidification); and,
Hydrogen Cracking is also called Delayed hydrogen cracking because the cracks can occur after many hours of the welding completion. Hydrogen cracking has been reported even up to 72 hours after welding has been completed.
Hydrogen Cracking Phenomena
The hydrogen dissociates (separate) in the arc and transforms in the atomic or ionized state into molten metal.
H2O = H2 + O, H2 = 2H, H = H+ + e–
The amount of hydrogen absorbed in weld metal depends on the hydrogen partial pressure and the temperature. Therefore, hydrogen solubility in the weld metal is 35ml H2/100g weld metal at 1800°C.
With decreasing temperature, the highest portion is again diffused. For iron, equilibrium solubility depends apart from temperature also on the lattice structure, on the type of elementary cell (CBC, CFC).
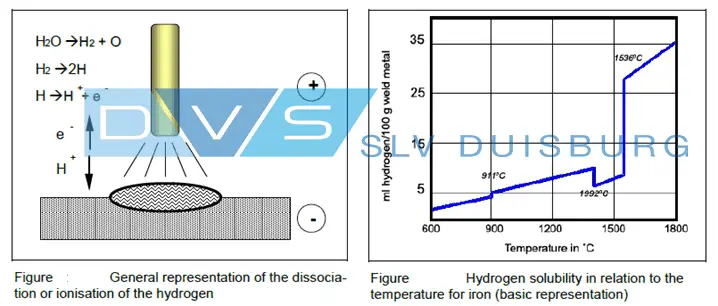
The figures above show the maximum hydrogen solubility that can be present in the weld metal even in the case of fast cooling.
But in fast cooling, it can be force-released molecular hydrogen embedded in the lattice cavities but also in spaces. Especially the element is concentrated in the range of dislocations and grain boundaries.
Because of its very low atomic radios (25 pm), (140 pm for iron), the hydrogen element is already being able to diffuse noticeable at room temperature. Now in microstructure and lattice areas with increased energy, the atomic hydrogen recombines into the gas molecules.
Due to recombination as well as a large number of hydrogen molecules in such microstructure areas, the hydrogen gas pressure rises strongly locally, thus the microstructure bonds can break apart locally resulting in pores or cracks.
This diffusion process, including recombination or dissociation mechanisms, can extend over periods lasting from minutes to several weeks.
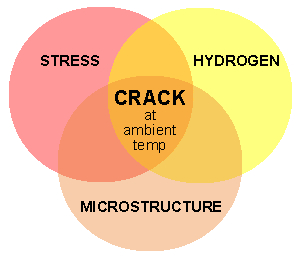
Factors Affecting the Formation of Hydrogen Cracks
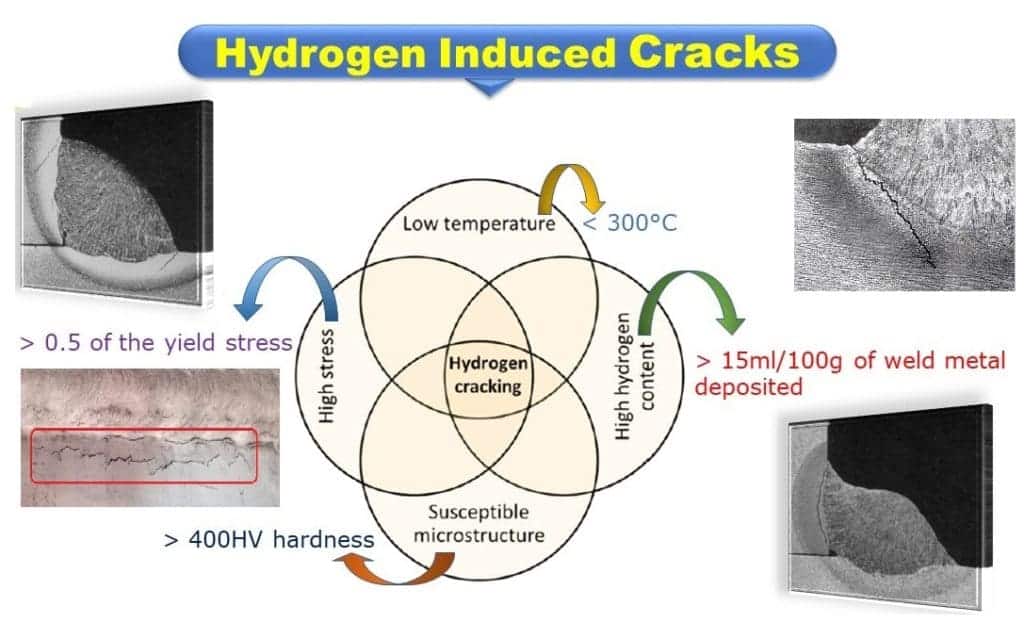
The risk of delayed cracking or hydrogen cracking depends on the following conditions:
- Level of hydrogen present in the weldment.
- Level of residual stresses in the welding
- Presence of hard microstructure phases (e.g. martensite).
How to Avoid Hydrogen Cracking
Hydrogen Cracking or delayed cracking or cold cracking can be prevented (avoided) by using careful welding consideration and following the good welding practices such as:
- Using properly baked and re-conditioned electrodes only.
- Use low hydrogen welding rods or process that deposit low hydrogen welds.
- Minimize the restrains on welding joints.
- Apply the right preheat temperature based on the alloy metallurgy, thickness and welding conditions.
- Control the interpass temperature.
- Avoid low heat input if possible. High heat input will let the weld to slow cool and gives time for hydrogen diffusion.
- Apply post weld heating for critical materials such as Cr-Mo alloys.