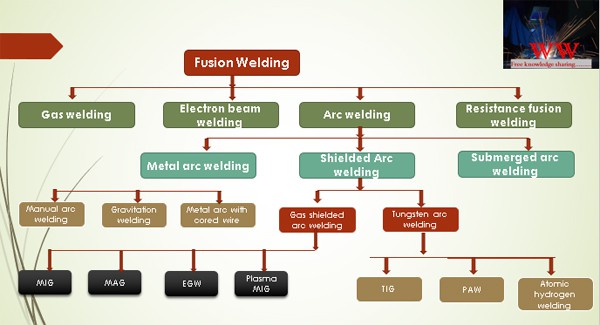
What is Flux cored arc welding or FCAW?
FCAW or flux-cored arc welding is a variant of Gas metal arc welding (GMAW) having a cored wired instead of solid wire being used in MIG-MAG Welding.
Definition/meaning of FCAW
FCAW means Flux Cored Arc Welding. FCAW is a type of Gas Metal Arc Welding (GMAW) having a cored wire instead of a solid wire that we see in the MIG-MAG welding process. FCAW definition can be given as ”a variant of gas metal arc welding where the filler wire is cored (hollow wire filled with flux) as shown in the below figure. FCAW wire is filled internally with flux while MIG/MAG (GMAW) wire is solid.

All remaining setup in FCAW is similar to gas metal arc welding. The wire is in the form of a spool. External shielding gas is used in FCAW-G variants. The wire is fed continuously and fed through the welding torch and nozzle to the welding arc.
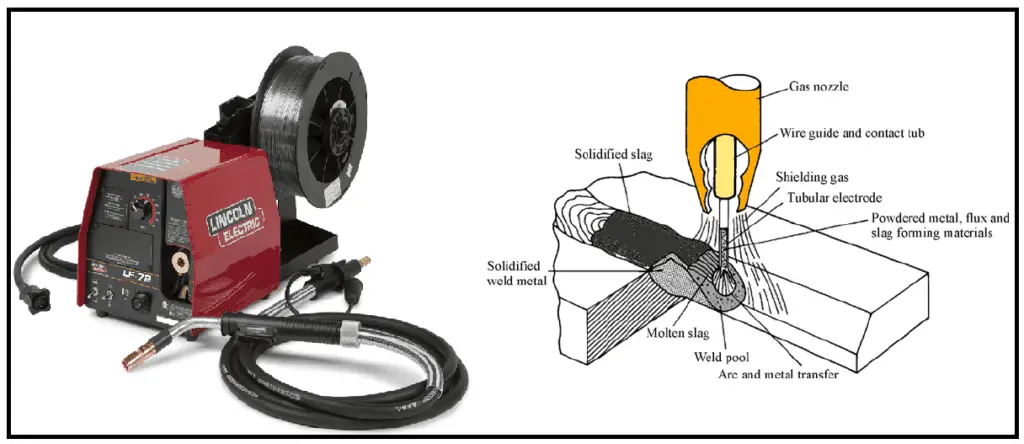
Flux Cored Arc Welding (FCAW) wire types
Flux Cored Welding wires are classified into three types:
- Gas shielded Types: The most used FCAW wires are gas shielded flux cored wire type. They require external gas shielding for welding. Generally, Pure carbon dioxide is used as shielding because of its low cost. Mixture of argon and CO2 are also used widely.
- The 2nd type of FCAW process variation is self-shielded flux-cored wire. Compared to first type, this variant of FCAW wire does not requires external gas shielding. The buring of coating produces the gases for protecting the weld pool. These type of wires are very beneficial for field applications or welding at height or home use.
- The third type of cored wires are metal cored wires. They are similar to flux cored wire but they do not contains flux inside the wire instead they are filled with metal powder and deoxidizers. Metal cored wires require external gas shielding like the first variant.
Designation & Classification of Flux-cored arc Welding (FCAW) Electrodes
The classification of FCAW wires is given in AWS A5.20 specification for carbon steel flux-cored arc welding wires (both self-shielded and gas-shielded). Classification of FCAW wire for low alloy steels, stainless steels, and surfacing are included in AWS Specifications A5.22 and A5.22 respectively.
Low alloy flux-cored arc welding wires classification is as per AWS A5.29 Specification. The classification system provides the wire mechanical properties, coating types, and welding characteristics. The electrode classification system for FCAW wire is given in the below diagram.
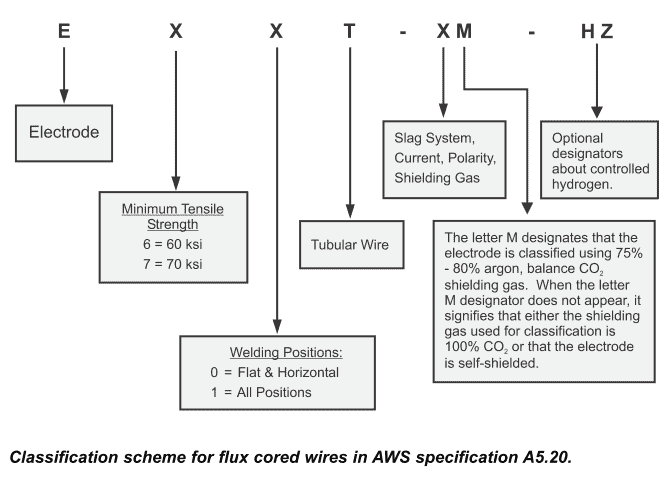

E71T-1C Electrode classification & its meaning
E71T1-C is a flux-cored arc welding wire used with CO2 gas shielding. The meaning of each digit in E71T1-C is:
- ‘E’ means- Electrode
- ‘7’ means- minimum tensile strength multiplied by 10 in Ksi, hence minimum tensile strength of 70Ksi.
- ‘1’ means- wire can be used for all positions. If there is ‘0’ instead of ‘1’, its mean wire can be used in flat & Horizontal properties to give the optimal properties & working.
- ‘T’ means- tubular. The wire is like a hollow tube, filled with flux inside. So, the name given as tubular.
- ‘1’ at this digit refers the welding wire usability characteristics. Other information about type of flux, coating type, polarity types etc.
- ‘C’ means- wire is used with Carbon Dioxide shielding gas. If M is given, its mean wire is used with mixture of argon + CO2 gas.
FCAW-S & FCAW-G Meaning
The difference between FCAW-S and FCAW-G is based on the presence of shielding gas. When we FCAW-S, ‘S’ means self-shielded. So, no external shielding gas is used in the Self-shielded mode of Flux-cored arc welding (FCAW).
The wire has sufficient coating elements to produce the shielding gases required to protect the weld pool. Examples of FCAW-S or self-shielded FCAW wires are- E70T-3, E70T-4, E70T-6, and E70T-10, etc.
FCAW-G is another variant of the FCAW where external shielding gas is mandatory during the welding to protect the weld pool. In FCAW-G, ‘G’ means Gas shielded. Externally supplied shielding gas (CO2 or mixture of argon + oxygen) is required to protect the weld pool from oxidation. Examples of FCAW-G type wires are- E71T1-C, E70T-1C, E70T-1M, and E71T-5C, etc. to name a few.
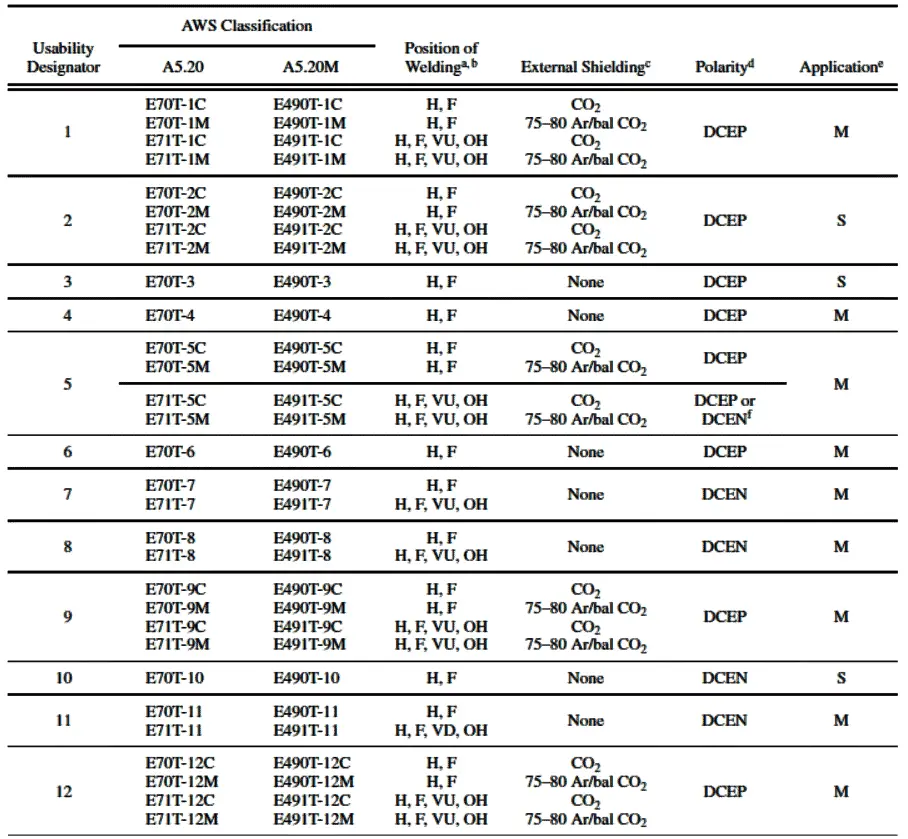
FCAW Welding Polarity
The polarity in FCAW welding depends on the type of welding wire. A detailed wire type and respective FCAW Welding polarity are given in the below picture.
FCAW wires E70T-1C,E70T-1M, E71T-1C, E71T-1M, E70T-2C, E70T-2M, E71T-2C, E71T-2M, E70T-3, E70T-4, E70T-6 are used with DCEP polarity. Most self-shielded flux-cored welding wires are used with DCEN Polarity.
Shielding gases for Flux-cored arc Welding (FCAW)
In flux-cored arc welding, the main types of shielding gas used are:
- Pure CO2
- Mixture of Argon =CO2
Pure CO2 is cheaper and can be used satisfactorily. Argon and CO2 mixtures are also used and they give fewer spatters during welding with improved weld toughness. Compared to pure CO2, the mixture of argon and CO2 is more costly.